Welcome to the Human Machine Interaction Laboratory
The Human Machine Interaction (HMI) Laboratory focuses on the design, control, implementation, and evaluation of mechatronic systems that are capable of haptic interaction — physical interaction with the user through the sense of touch. In particular, we develop and analyze principles and tools to enable physical human-robot interaction (pHRI) with a systems and controls perspective. We aim to achieve optimal performance for such systems, while simultaneously ensuring the safety and ergonomic nature of interaction under the coupled dynamics of the human-robot system and the constraints imposed by human biomechanics/sensorimotor control. Our research extends to synthesizing algorithms for simulated physical interaction with virtual environments (haptic rendering) and exploring the control theoretical framework of the human sensorimotor system through empirical investigations of skill acquisition.
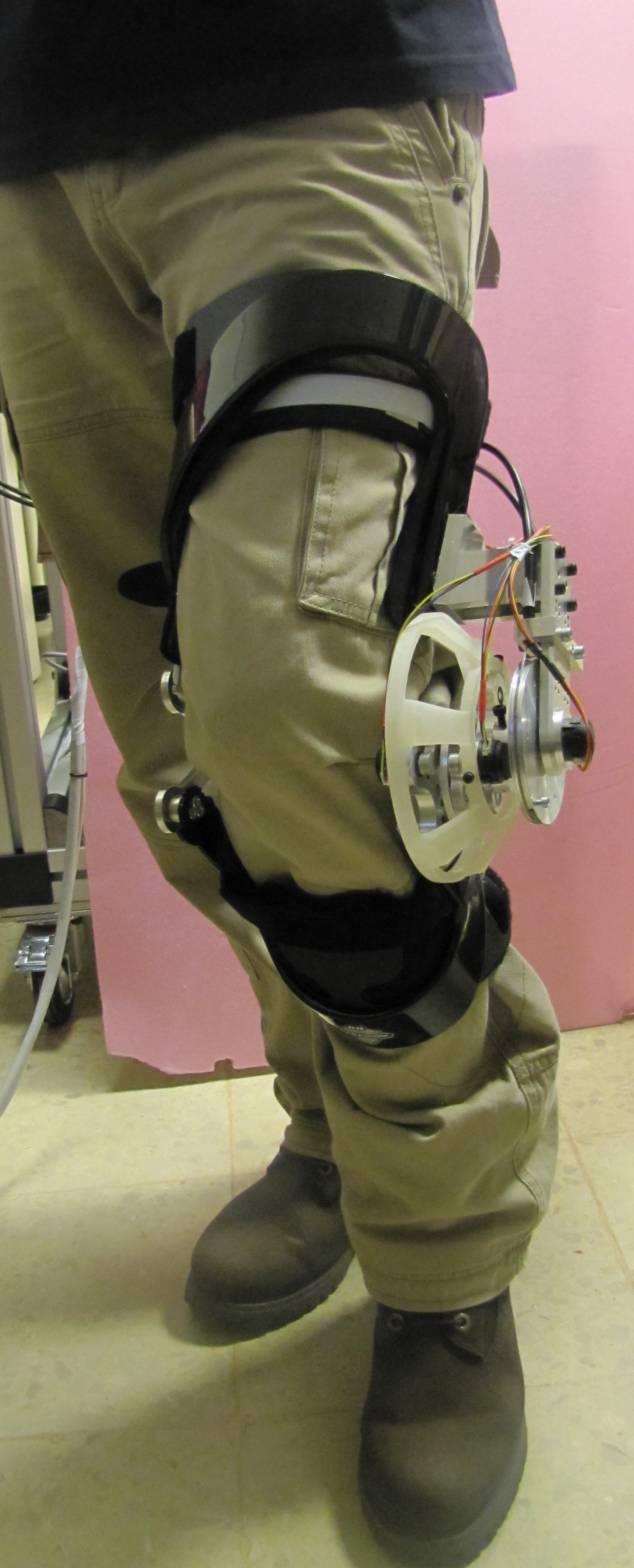
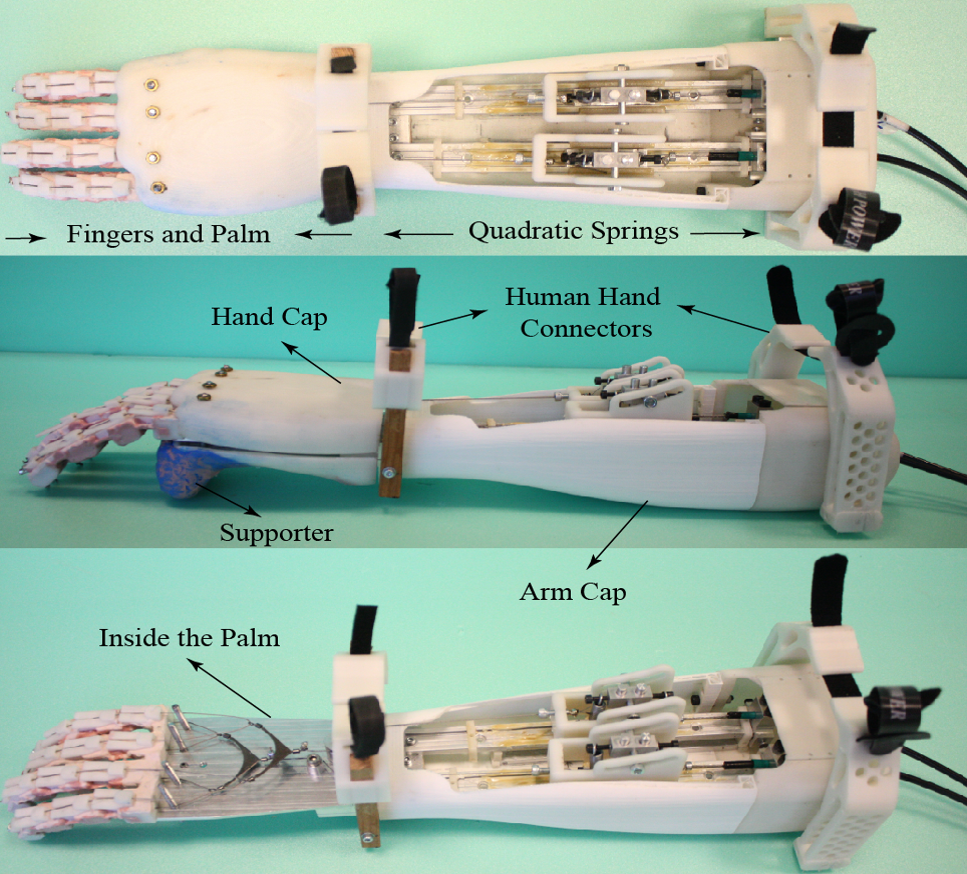
Applications of our research include robotic devices for physical rehabilitation, active exoskeletons and prostheses for human augmentation, force-feedback devices for robot-assisted surgery, haptic interfaces for manual skill training, teleoperators for exploration of hazardous or remote environments, x-by-wire systems for automotive/aerospace industry, and service robots for collaborative task execution with humans.
Our research contributes to the fields of robotics, systems and controls, multi-body dynamics, mechanical design, biomechanics, physical medicine, and basic science.
The HMI Lab is directed by Prof. Volkan Patoglu, and is part of the Mechatronics Engineering Program of Sabanci University.
We are looking for passionate new PhD students, Postdocs, and Master students to join the team (more info) !